

EXPLICAMOS
ESTE TEMA ES SOBRE FUNCIÓN CUADRÁTICA, EN ESTA SECCIÓN ENCONTRARÁS INFORMACIÓN PARA ENTENDER EL TEMA Y SABER CÓMO APLICARLO , TE INVITO A QUE DISFRUTES Y QUE AL TERMINAR CONTINÚES AL EXPLORAMOS CON LAS FLECHAS EN EL INFERIOR.
Representación gráfica de la parábola
Para construir una gráfica de parábola se requiere conocer los siguientes elementos:
Por el vértice pasa el eje de simetría de la parábola, es decir, cuando el coeficiente del término es positivo el vértice será el punto más bajo de la gráfica y las fórmulas para encontrarlo son las siguientes:
Así mismo, la ecuación del eje de simetría es:


Puntos de corte con el eje X
Para encontrar el valor de x cuando f(x)=0, la segunda coordenada debe igualarse a cero, por lo que tendremos que resolver la siguiente igualdad:
Al resolver la ecuación anterior los resultados pueden ser:
-
Dos puntos de corte: (X1, 0) y (X2, 0) esto sucede si b - 4ac >0
-
Un punto de corte: (X1,0) esto sucede si b - 4ac = 0
-
Ningún punto de corte si b - 4ac <0

Puntos de corte con el eje Y
Para encontrar la intersección con el eje la primera coordenada debe igualarse a cero, , por lo que tendremos:
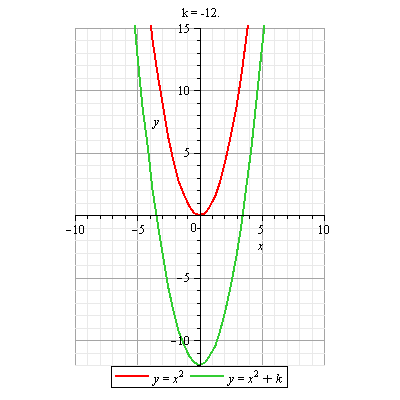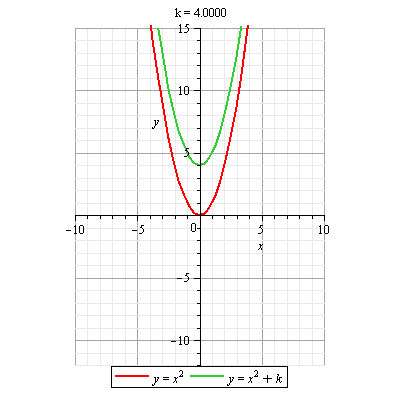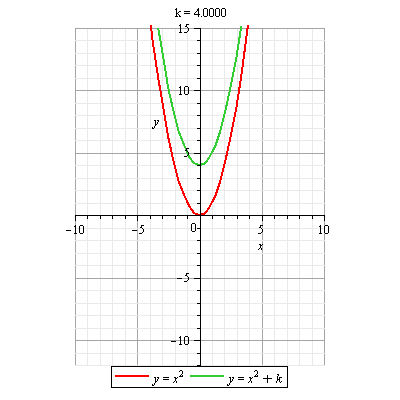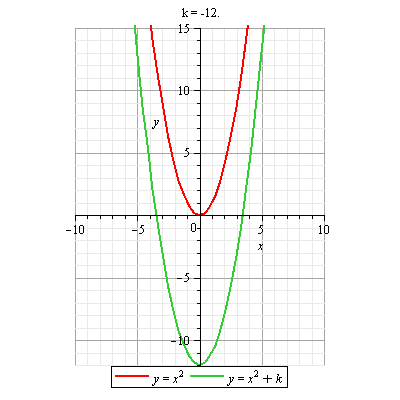
DOMINIO DE UNA FUNCIÓN
Como con cualquier función, el dominio de función cuadrática f ( x ) es el conjunto de los valores de x para los cuales la función esta definida, y el rango es el conjunto de todos los valores de salida (valores de f )













