
Las características estudiadas de la función potencia, permiten modelar algunas situaciones de la vida cotidiana y fenómenos de distintas áreas del conocimiento como, biología, economía, geología, entre otros.
Modelar una progresión geométrica por medio de una función potencia
Si te fijas en el término general de una progresión geométrica de la forma an = a1 r(n-1), corresponde a una función potencia de la forma f (x) = axn-1, ya que si las comparas, f (x) representa el término n – ésimo, que tiene como razón x y como primer término a, por lo tanto, podrás modelar cualquier progresión geométrica por medio de la función potencia.
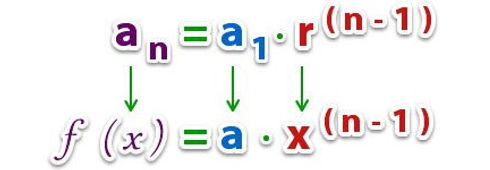
Ejemplo 1:
Dada la función f (x) = 2x10, y la progresión geométrica 2, 4, 8, 16, 32…
Determina el onceavo término de la progresión geométrica.
Si te fijas, con la función dada como esta elevada a diez, nos permite conocer el onceavo término de la progresión geométrica, donde su primer término es 2, cuya razón es x.
Reemplazamos, por la razón de la progresión geométrica que es 2.

Respuesta: El onceavo término de la progresión geométrica es 2048.
Ejemplo 2:
Tres colonias de bacterias incrementan su cantidad al doble, al triple, o al cuádruple, respectivamente cada hora. Si al comienzo de la propagación en cada colonia había 150 bacterias, ¿cuántas bacterias habrá después de 6 horas en cada caso? Determina el modelo con respecto a la función potencia.
Como la cantidad inicial de bacterias en los 3 casos es de 150, y se pide la cantidad de bacterias después de 6 horas, podemos modelar el crecimiento a través de la función potencia de la forma.
Entonces, como la tasa de crecimiento es x, reemplazamos en los tres casos (con 2, 3 y 4


Respuesta:
En la colonia de bacteria que se duplica habrá después de 6 horas 4.800 bacterias, en la que se triplica 36.450 y en la que se cuadruplica 153.600.
Modelar el interés compuesto por medio de una función potencia y sus traslaciones
Podemos modelar situaciones de interés compuesto, utilizando la función potencia de la forma;

Si te fijas, f(x) corresponde al capital final (Cf), a al capital inicial invertido (Ci), x al a la tasa de interés compuesto (i) y t al período de tiempo (t) de la inversión.
Ejemplo 1:
Javiera quiere invertir $ 100.000 a una tasa de interés compuesto anual del 20 % por 2 años. ¿Con que función potencia podemos modelar la tasa de interés? ¿Cuál será el capital final?

Ahora, para la tasa de interés x = 0,20 el capital final es;

El capital final es $144.000.-
Nota: También puedes graficar diferentes situaciones que involucren la función potencia a través de diferentes software, como por ejemplo GeoGebra, si ingresamos los datos de la función podremos obtener los mismos resultados
pero vistos en gráficos.












